Graph Signal Processing
Introduction
Signals are everywhere. In the present world, signal processing is likely to be changing into information processing with the introduction of new research trends like Topological signal processing, Graph signal processing, Data-Driven approaches for imaging systems (including neural networks), Data-Driven beamforming techniques for 6G and Beyond communication systems, latest video compression standard VVC and some new ones to many models like Multimodal Speech recognition. Thanks to some ground-breaking inventions such as the Fast-Fourier Transform, linear filters, and Kalman filter, which are distinctive to open the pathway of such overwhelming trends. Here, we are going to do a brief discussion on Graph signal processing.
First of all, what is signal processing? Why is it considered to be one of the pioneering fields for research? The answers to these questions lead us to the following discussion. The representation, analysis, and manipulation of signals are dealt with within the field of engineering and applied mathematics, known as signal processing. Any quantity that carries information is a signal, including time-varying voltages, sound waves, and images. Signal processing’s objective is to extract information from signals and portray it in a more practical and understandable manner. Filtering, Fourier analysis, compression, and feature extraction methods are used to achieve this. Numerous industries, including telecommunication, voice and image processing, control systems, and biomedical engineering, use signal processing in various ways. Signal processing uses mathematical techniques and models to analyze and alter signals to extract useful information, enhance signal quality, or decrease the quantity of data required to describe the signal. As the requirements and capacities of different application areas evolve, new approaches are continually being created in the sector.
Graph Signal Processing
Data is everywhere in massive quantities in the present technological world. Almost every aspect of our day-to-day life is recorded at one or many different kinds of levels. Our personal health data are recorded and processed through health monitoring devices and apps, various types of financial and banking data, our web searches, our social networks, and our mobility by traffic patterns. Each of these data is being recorded by any means. The complexity of such networks and interactions means that the data now resides in more irregular and complex structures. So to process these kinds of complex data into precise, meaningful information, we need new tools.
In Simple words, Graph signal processing (GSP) can be briefly described as a branch of signal processing, concerned with the study and control of signals defined on graphs. The interactions between the signal samples in GSP are modeled as graphs, which may subsequently be examined using graph spectral theory, graph filters, and other graph-based processing methods. In order to handle signals with underlying structures such as those that emerge in social networks, brain connections, and other complex systems, GSP aims to expand the capabilities of conventional signal processing techniques.
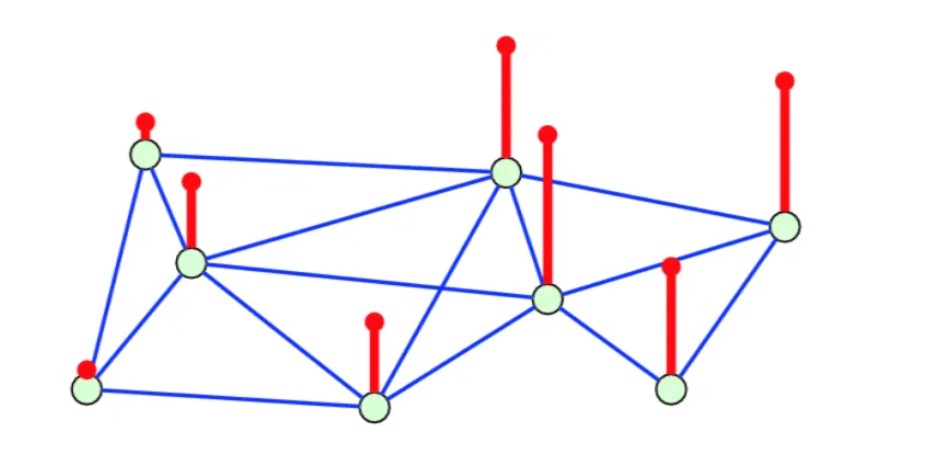
Graph Signal. Source: https://link.springer.com/chapter/10.1007/978-3-030-03574-7_1
For example, let us consider a state which has 8 cities. Suppose we need to represent the number of automobiles in each city. As shown in the figure, we can represent this information as a graph. Each light green vertex represents a city and its location in the state. The route between the two connected cities might be interpreted as the boundaries separating the cities. The number of vehicles, a scalar value, is represented by the red vertical line. Therefore, as the red line rises, so does the city’s automotive population.
Graphs offer the ability to model such complex data and interactions between them. The data can be modeled into nodes and edges. Graph signal processing introduces exploration and analysis of such nodes and edges by adding attributes and modeling those as signals on a graph. For example, the temperature in a given city on a given day in a weather network. Representing such data into graphs requires us to extend classical signal processing concepts and tools such as Fourier Transform, Filtering, and frequency response to data residing on Graphs. It also leads us to tackle complex tasks such as sampling in a principled way.
Classical signal processing signals can stem from various domains. However, the underlying graphs can tell a fair amount about those signals through their structure. Different types of Graphs model different types of data and complex networks. Such graphs include Erdos-Renyi graphs, ring graphs, random geometric graphs, small-world graphs, and scale-free graphs. As in classical signal processing, graph signals can have properties such as smoothness that needs to be appropriately defined. They can also have spectral representation. In particular, the Graph Fourier Transform allows us to develop intuition gathered in the classical setting and extend it to graphs; we can talk about the notions of frequency band limitedness, for example, we can filter graph signals. They can be sampled, we can denoise graph signals, learn their underlying structure, and model them.
Additionally, there is a lot of promise for Graph Signal Processing to be used in sensor networks, smart grids, medical neural networks, the internet of cars, and other areas. Graph Signal Processing techniques are frequently implemented on the network using a single processing center in a centralized fashion. The centralized processing solution offers the benefits of being simple to implement and flexible when scheduling resources.
However, when the scale of the network grows, the centralized approach’s computational complexity quickly rises, necessitating more expensive gear. Additionally, the network as a whole may become paralyzed if the central node is attacked from the outside.
References
[1] A. Ortega, P. Frossard, J. Kovačević, P. Vandergheynst, and J. M. F. Moura, “Graph Signal Processing: Overview, challenges, and applications.” [Online], 2018. Available: https://ieeexplore.ieee.org/document/8347162.
